応力とひずみの関係とは？関係式、計算方法を理解して機械設計に活かそう！｜機電系エンジニア専門の求人情報サイト

">>

応力とひずみの関係とは？関係式、計算方法を理解して機械設計に活かそう！

2024.08.06更新

機電系エンジニア必見！！貴重なフリーランス案件はこちら ▶

この記事を書いた人

長谷川

FREE AID編集部機電系専門ライター Div.
アナログ回路設計・営業を経験した後ライター＆ディレクターとして独立。
電気電子・ITジャンルを得意とし、正確で分かりやすい情報の発信を行っています。

機械設計において、強度評価をする際の基礎知識の一つが材料力学ですが、その中でも応力とひずみの関係は最も初歩的かつ重要な知識です。CAEの応力計算などでもこの関係式が使われるので、機械設計初心者の方は本記事の内容をぜひ参考にしてみてください。

応力とひずみの基礎

応力とは

「応力」は物体に力が働いた場合に、物体内部に発生する単位面積（1 m^2）当たりに作用する力を示した値です。特に機械設計の分野において応力は、部材の変形や破壊を評価する際に用いられる物理量を示します。表記に用いられる記号は、シグマ（σ）です。応力の単位はSI単位系では[N/m^2]、または[Pa]で表します（1N/m^2 = 1Pa)。ただし機械設計などの実務では、mよりもmmが多用されます。

応力には部材に働く荷重の向きによって、「引張・圧縮応力」「せん断応力」「曲げ応力」などの呼び方がありますが、単位はどれも同じです。引張応力に対して圧縮応力は負の値で表されます。部材の破壊を評価する際には、これらを組み合わせた応力と、部材が許容する応力値を比較して評価します。ただし、荷重の向きによって許容する応力は異なるため、向きや種類の異なる応力が負荷された状態を評価する際には注意が必要です。

ひずみとは

「ひずみ」は、物体に力が働いた場合の物体の変形量を、変形前の寸法に対する比率として示した値です。部材に力が働いた際の、部材の変形量を評価する場合に用いられます。表記に用いられる記号はイプシロン（ε）です。ひずみは、変形前後の長さの比率であるため、単位のない無次元量で表されます。

ひずみも応力と同様に、部材に働く荷重の向きによって、「引張・圧縮ひずみ」「せん断ひずみ」があります。引張ひずみに対して圧縮ひずみは負の値で表記可能です。

応力の求め方

応力には荷重の向きによって、引張・圧縮、せん断、曲げ応力に分類されます。本章では、各応力の公式を示します。なお「ひずみ」の値は、後述する「フックの法則」によって応力値から算出できるため、この章では省略します。

引張・圧縮応力の求め方

引張・圧縮応力は材料力学などの計算に使用されるさまざまな応力の中で、最も基礎的な概念です。引張・圧縮応力は、働いた力と同じ方向に働く応力で、ある断面に働く軸方向の力（N）を断面積（A）で除した値と定義されます。引張・圧縮応力値の公式は、以下の関係式で表されます。

引張・圧縮応力の公式

σ = N/A [N/mm^2]

せん断応力の求め方

「せん断」とは、ある部材を「はさみ切る」ように作用する現象のことです。物体の断面に対して平行に、互いに反対向きの一対の力を作用させると物体はその面に沿って滑り切られる力を受けますが、これが「せん断力」です。文具の「ハサミ」も、この「せん断力：Q」を使ってモノを切断しています。せん断力により物体の断面に生じる応力が「せん断応力：τ」です。せん断応力の公式は、以下の関係式で表されます。

せん断応力の公式

τ = Q/A [N/mm^2]

曲げ応力の求め方

曲げ応力は、細長い棒状の構造物（はり）に、断面に垂直な横荷重が作用することで、はりが曲げられる際に発生する応力です。横荷重が作用すると断面には「曲げモーメント：M」と「せん断力：Q」が発生し、それぞれ「曲げ応力：σ」と「せん断応力：τ」となります。ただし、それぞれの応力の方向が異なることに加え、せん断応力よりも曲げ応力の方が支配的となるため、曲げ応力のみが考慮される場合が多いです。

また、曲げ応力は断面の位置によって値が異なります。上端と下端部で最大または最小値となり、中間では上端と下端部から線形で推移します（上下対称の断面では中心で0となる）。曲げ応力の公式は、以下の関係式で表されます（以下の式は最大値を示す）。関係式における断面係数は、断面の形状によって決まる値ですが、本記事では説明を省略します。

曲げ応力の公式

σ = M/Z [N/m^2] Z：断面係数 [mm^3] M：曲げモーメント [N・mm]

【機電系エンジニア必見！】フリーランス案件掲載中▶

応力とひずみの関係

応力とひずみの関係は、縦軸に応力値を、横軸にひずみを記した、「応力－ひずみ曲線」で表されます。応力－ひずみ曲線は、引張試験機を用いて計測したい材料で作られた試験片を引っ張る「引張試験」によって実験的に求められる曲線です。試験片の形状は、日本工業規格（JIS）で定められています。

また、ひずみには変形前の長さに対するひずみ値である「公称ひずみ」と、変形後の長さを変形前の長さで割って自然対数を取る「真ひずみ」があります。材料力学などの計算で考慮する「微小変形問題」を計算する場合は公称ひずみを用い、変形を無視できない「大変形問題」を計算する場合には、真ひずみを用います。

鋼材の場合

鋼材における応力－ひずみ曲線

以下に鋼材における応力とひずみの関係を示した、応力－ひずみ曲線を示します。下図の、ひずみは公称ひずみです。縦軸の応力は試験片に働く「力」に比例し、横軸のひずみは試験片の「伸び」に比例します。つまり応力－ひずみ曲線は、部材に働く力と変形量の関係を示した図です。

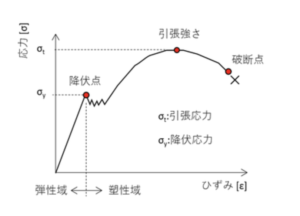
弾性変形と塑性変形

応力とひずみは、ある値まで比例関係にあり、この範囲を「弾性域」といいます。弾性域の変形を「弾性変形」と呼び、この範囲では働いている力を無くすと（除荷）元の状態に戻ります。一方で、比例関係ではなくなる範囲を「塑性域」といいます。塑性域では働いている力を無くしても、完全に元の状態には戻りません。これを「永久変形」といいます。

降伏点と引張強さ

鋼材の場合、応力とひずみの比例関係が終わる「降伏点」が発生します。降伏点の応力値は「降伏応力：σy」と呼ばれます。降伏応力は材料が永久変形しない範囲でもあるため、機械設計では強度評価における許容応力値として用いられます。一方で、降伏点を越えてひずみを増やしていくと応力が最大となる点があります。この最大となる応力値を「引張強さ：σt」といいます。

引張強さは材料が受け持つことのできる最大応力値であるため、こちらも強度評価における許容応力値に用いられます。「降伏応力」を許容値にする場合は、製品を使用するうえで、日常的に発生する荷重に対する強度評価に使用されます。一方で「引張強さ」は、製品を使用するうえで、発生する頻度は低いが無視できない最大荷重に対しての許容値として、破壊を起こさないことを保証するための強度評価などに使用されます。

鋼材以外の延性材料の場合

鋼材以外の延性材料における応力－ひずみ曲線

「延性材料」とは力を加えると伸びる性質を持つ材料で、アルミニウム合金や銅合金などに加えて、プラスチックやゴムなどの材料が含まれます。反対に、ガラスやコンクリートなどの力を加えても伸びない材料を「脆性材料」といいます。以下に鋼材以外の延性材料における応力とひずみの関係を示した、応力－ひずみ曲線を示します。下図のひずみは鋼材と同様に公称ひずみを示します。

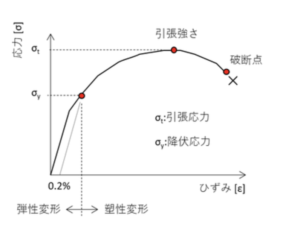
耐力

鋼材以外の延性材料には弾性域と塑性域を区別する「降伏点」が発生せず、緩やかに塑性域に遷移します。そのため、鋼材以外の延性材料の場合、0.2％のひずみが残る範囲を弾性域と定義します。0.2％のひずみとは、1000mmの長さの部材の場合、1002mmになるときのひずみです。この場合は除荷した際に元の長さに戻らず0.2％のひずみ（1000mmの場合は2mm）が残ります。

鋼材の「降伏応力」に対して、鋼材以外の延性材料における0.2％のひずみが発生する応力値を「耐力」といいます。耐力は降伏応力と同様に、機械設計の強度評価における、弾性変形域での許容応力値として用いられます。

応力とひずみの関係式

フックの法則とヤング率

材料力学において、弾性域で応力とひずみが比例関係となることを「フックの法則」といいます。また弾性域において、応力－ひずみ曲線の傾きが「ヤング率：E」です。応力－ひずみ曲線から、弾性域の傾きが大きくなる（ヤング率が大きくなる）とひずみ（変形）に対する応力値（力）が大きくなります。

つまり、ヤング率が大きくなると変形しづらくなります。ヤング率は材料の変形のしにくさである「剛性」を示す指標であり、材料固有の値です。フックの法則が成立する弾性域において、応力とひずみ、ヤング率はそれぞれ以下の関係式で表されます。

フックの法則における応力とひずみの関係式

σ = E × ε [N/mm^2] 　σ：応力 [N/mm^2] 　E：ヤング率 [N/mm^2] 　ε：ひずみ [％]

ポアソン比

ポアソン比（ν）は、弾性域において材料に応力を加えたときに、力が働く方向に働くひずみと、力に対して垂直方向に働くひずみの比を示します。ポアソン比は、ヤング率と同様に材料固有の値であり、実験的に求められる値です。

例えば、単純な形状の2次元の長方形の板を考えます。長辺方向に応力：σxが働くように板を引っ張ると、長辺方向のひずみ：εxが発生します。このとき短辺方向には、圧縮方向のひずみ：εyが発生します。この板におけるポアソン比の定義とひずみの関係は、以下の式となります。

ポアソン比とフックの法則

ν = – εx/εy εx = σx/E εy = – ν × σx/E （いずれも無次元量）

機電系エンジニア活躍中！フリーランス高単価案件はこちら ▶

応力とひずみの関係を把握して機械設計に役立てよう

機械設計における強度評価をするうえで、応力とひずみの関係はもっとも初歩的かつ避けては通れない概念です。昨今の機械設計プロセスでは、CAE(Computer Aided Engineering)を取り入れることが増えていますが、CAEの応力評価に用いられるFEM(Finite Element Method)は、弾性域におけるフックの法則から、材料の応力や変形量を計算します。

強度評価以外でも機構解析における部材の微小弾性変形の計算などでも、応力とひずみの関係は使われています。これから機械設計におけるCAEやFEMの技術を習得しようとしている設計初心者の方は、ぜひ本記事の内容を学習し、機械設計業務に役立てましょう。

フリーランス×機電系エンジニア！高単価求人はこちら ▶

応力とひずみの関係とは？関係式、計算方法を理解して機械設計に活かそう！のページです。エンジニアにまつわるお役立ちの最新情報を発信しています。電気電子設計や製造技術や機械設計・生産技術などはもちろん、フィールドエンジニアやITシステム開発まで、機電系エンジニア業界での働き方や年収、話題性の高い情報を細かく解説しています。また、当サイトではフリーランス機電系エンジニア求人をご用意しています。気になるエンジニア求人があれば、ご応募ください。フリーランスの機電系エンジニア求人なら【フリーエイド】

前の記事を読む

記事一覧に戻る

次の記事を読む

こんな記事も
合わせて読まれています

- AI（人工知能）の種類一覧｜定義や特徴・目的に合わせたシステムの違いをご紹介

機電系求人はこちら

TOP>
記事一覧>
応力とひずみの関係とは？関係式、計算方法を理解して機械設計に活かそう！